22 Oct 2012
Combinatorial Optimization
The purpose of combinatorial optimization is, in plain english, to find an optimal value in a finite set of said values. Usually it means finding the minimum or the maximum of a given function or problem space. Now, the fun part is that there are many problems where brute-force searching is not feasible due to the vast size of the set possible values. Some classical computer science problems like this are the Traveling Salesman Problem and Minimum Spanning Tree.
This has a lot of practical applications, some of them are (quoting Wikipedia):
- Developing the best airline network of spokes and destinations
- Deciding which taxis in a fleet to route to pick up fares
- Determining the optimal way to deliver packages
- Determining the right attributes of concept elements prior to concept testing
In this post I write about one of the many possible algorithms to tackle this kind of problem, it is called Simulated Annealing.
Annealing
Annealing in metallurgy is a process in which certain metals are altered to improve certain properties like hardness and ductility.
The process consist of heating the material to very high temperatures (depending on the material) and letting it cool down gradually allowing its atoms to progress into its equilibrium state. This heating process alters the internal structure of the material resulting in a more uniform composition of the atoms, hence improving hardness and ductility.
Simulated Annealing
This algorithm is a meta-heuristic, what that means is that it doesn’t guarantee a solution since it searches for a good approximation in a small amount of time by iteratively improving it.
These problems are represented as a solution space, a starting state (initial solution) and a function that calculates the “goodness” or “energy” of a solution.
The analogy with annealing is that the algorithm starts with a given temperature and a random solution and iteratively calculates a new random solution. A solution is selected depending on the result of a probability function that takes into account if the solution is better or worse than the current accepted solution and the temperature. As the temperature decreases, the probability of accepting worse solutions also decreases. Also, an “stabilization” period happens between changes in temperature to allow the system to stabilize.
Simulated Annealing Javascript:
function _probabilityFunction (temperature, delta) {
if (delta < 0) {
return true;
}
var C = Math.exp(-delta / temperature);
var R = Math.random();
if (R < C) {
return true;
}
return false;
}
function _doSimulationStep () {
if (currentSystemTemperature > freezingTemperature) {
for (var i = 0; i < currentStabilizer; i++) {
var newEnergy = generateNeighbor(),
energyDelta = newEnergy - currentSystemEnergy;
if (_probabilityFunction(currentSystemTemperature, energyDelta)) {
acceptNeighbor();
currentSystemEnergy = newEnergy;
}
}
currentSystemTemperature = currentSystemTemperature - coolingFactor;
currentStabilizer = currentStabilizer * stabilizingFactor;
return false;
}
currentSystemTemperature = freezingTemperature;
return true;
}The code is pretty straightforward: While the temperature is above freezing, generate a neighbor (new solution based on our current one) and calculate the delta of the goodness of that solution against the goodness of our current solution, if the probability function returns true accept the solution.
I won’t go into much detail on the selected probability function but I will show a graph of the behavior just so we can be sure that it meets our criteria:
- A better solution is always accepted.
- A worse solution has less chance to be accepted than a “not so worse” solution.
- Worse solutions (regardless of “worseness”) have less chance to be accepted as temperature decreases.
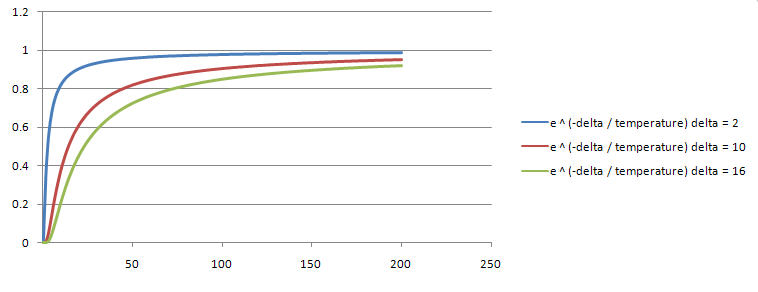
The larger the delta the worse the generated solution is compared to our current accepted solution.
Eight Queen Puzzle
The puzzle is about placing eight chess queens on an 8x8 chessboard so no two queens can attack each other, that is, they cannot share the same row, column or diagonal with each other.
There are 4,426,165,368 possible arrangements of eight queens on a 8x8 board but only 92 solutions. The problem is not trivial, although by today hardware standards even a brute force approach would probably do fine, specially if you reduce the problem space a bit like adding the restriction that queens cannot share columns or rows and you reduce the number of possibilities to 16,777,216 but for the sake of showing the algorithm let’s use the problem as it is.
To represent the puzzle I am simply going to use an array of eight elements with x and y as properties and to plug the problem into the simulated annealing implementation we need just a few functions, the first and probably most important we need a way to calculate the number of attacks between queens in any given configuration. Our goal is to optimize the result of this function:
// Simply count the queens that share row, column or diagonals.
function _calculateAttacks (board) {
var numAttacks = 0;
for (var iQueen = 0; iQueen < NUM_QUEENS - 1; iQueen++) {
for (var iAttackingQueen = iQueen + 1; iAttackingQueen < NUM_QUEENS; iAttackingQueen++) {
if (board[iQueen].x == board[iAttackingQueen].x) {
numAttacks++;
}
else if (board[iQueen].y == board[iAttackingQueen].y) {
numAttacks++;
}
else if (board[iQueen].x + board[iQueen].y ==
board[iAttackingQueen].x + board[iAttackingQueen].y) {
numAttacks++;
}
else if (board[iQueen].y - board[iQueen].x ==
board[iAttackingQueen].y - board[iAttackingQueen].x) {
numAttacks++;
}
}
}
return numAttacks;
}For the operation of the algorithm we need three functions.
- Generate a random initial solution.
- Generate a “neighbor” solution, that is, based on our current configuration just change it slightly, so we don’t do huge jumps along the search space, we achieve this by taking a random queen and moving it a single step in a random direction.
- Accept the neighbor if simulated annealing determines so.
// Generate 8 queens with random (x, y) and no repetitions. No queen can share the same space as another one.
function _generateRandomPositions () {
var done = false;
for (var iQueen = 0; iQueen < NUM_QUEENS; iQueen++) {
var repetitions = true;
currentQueensPositions[iQueen] = {};
while (repetitions) {
currentQueensPositions[iQueen].x = parseInt(Math.random() * 8);
currentQueensPositions[iQueen].y = parseInt(Math.random() * 8);
if (!_checkRepetitions(currentQueensPositions)) {
repetitions = false;
}
}
}
return _calculateAttacks(currentQueensPositions);
}
// Take our current solution and generate a neighbor solution by taking a random queen and moving it a single random step.
function _generateNeighbor () {
for (var iQueen = 0; iQueen < NUM_QUEENS; iQueen++) {
newQueensPositions[iQueen] = {
x: currentQueensPositions[iQueen].x,
y: currentQueensPositions[iQueen].y
};
}
var changingQueen = parseInt(Math.random() * NUM_QUEENS);
var repetitions = true;
while (repetitions) {
var oldX = newQueensPositions[changingQueen].x;
var oldY = newQueensPositions[changingQueen].y;
// The MOD is so if a queen moves out of the board it comes through the other side. The extra mod logic is to avoid a javascript bug
// that makes negative numbers mod into -1.
newQueensPositions[changingQueen].x = (((newQueensPositions[changingQueen].x + (parseInt(Math.random() * 3) - 1)) % 8) + 8) % 8;
newQueensPositions[changingQueen].y = (((newQueensPositions[changingQueen].y + (parseInt(Math.random() * 3) - 1)) % 8) + 8) % 8;
if (!_checkRepetitions(newQueensPositions)) {
repetitions = false;
}
else {
newQueensPositions[changingQueen].x = oldX;
newQueensPositions[changingQueen].y = oldY;
}
}
return _calculateAttacks(newQueensPositions);
}
// Accept the current generated solution.
function _acceptNeighbor () {
for (var iQueen = 0; iQueen < NUM_QUEENS; iQueen++) {
currentQueensPositions[iQueen] = { x: newQueensPositions[iQueen].x, y: newQueensPositions[iQueen].y } ;
}
}Sample implementation
And without further ado, running code (if you are reading this on a rss reader you won’t be able to see this, please go to website, I apologize):
Play around with the parameters!
Pretty simple code, it still amazes me how simple the simulated annealing code is and that it still gets the right answers most of the time given good parameters. The parameters for this particular implementation I found simply by trial and error and experimentation, even the original paper suggest that but certainly there may be better ways to determine them for a given particular problem.
The full source code is available here feel free to play around with it and if you find a bug let me know, I wrote this code some years ago.